教室では、生徒たちが一歩ずつ課題に向き合い、確実に力を伸ばしています。
この記事では、リードアップでの授業内容や学習の取り組みをお届けします。
塾に通っていない方にとっては「リードアップの学習スタイル」や「伸びる理由・成果につながる仕組み」を知るきっかけに。
塾生・保護者の方にとっては、お子さまがどんなことに挑戦しているのかを知っていただき、「ご家庭での声かけ」や「学習サポート」に役立つ情報としてご活用いただければ幸いです。
小学5年生

まずは小5・6生、中1・2生です!

【算数】倍数と公倍数/約数と公約数

5年生は倍数と公倍数、約数と公約数を中心に学習をしました。
これらの単元はしっかり理解をしておかないと、今後の「分数のたし算・ひき算」6年生で習う「分数のかけ算・わり算」でつまづいてしまうことになります。
しっかりと理解して進みましょう!
倍数の見分けかたには、いくつかのコツがあります。
これらの知識を知っておくと、今後の分数の問題が劇的に楽になります!
ぜひ覚えておいてください。
倍数の見分け方
2の倍数(=2で割りきれるかどうか)の見分け方
1の位(下1ケタ)が偶数(2,4,6,8…)または「0」になっていれば、その数は2の倍数になる。
例) 「96」=2×48 「154」=2×77
3の倍数の見分け方(=3で割きれるかどうか)
すべてのケタの数字を合計した数(各位の数の和)が3の倍数になっていれば、もとの数も3の倍数になる。
例) 「162」 1+6+2=9(各位の数の和)、162=3×54
4の倍数の見分け方(=4で割きれるかどうか)
下2ケタを2ケタの数字とみてそれが「00」または4の倍数なら、もとの数も4の倍数になる。
例)「1500」=4×375 「1936」=4×484
4の倍数は2の倍数なので、2の倍数でなければ4の倍数かどうかを確認する必要はない!
5の倍数の見分け方(=5で割きれるかどうか)…
1の位が「0」か「5」になっていればその数は5の倍数になる。
例) 「75」 =5×15 「1250」 =5×250
6の倍数の見分け方(=6で割きれるかどうか)
2の倍数と3の倍数の見分け方の両方をクリアしている数は6の倍数になる。
例)「1464」…1の位の数が偶数(=2の倍数)、かつ各位の数の和が3の倍数[1+4+6+4=15](=3の倍数)なので、1464は6の倍数(6×244)
8の倍数の見分け方(=8で割きれるかどうか)
下3ケタが8の倍数ならもとの数も8の倍数になる。
例) 「2320」 =8×290
9の倍数の見分け方(=9で割きれるかどうか)
すべてのケタの数字を合計した数(各位の数の和)が39の倍数になっていればもとの数も9の倍数になる。
例) 「198」 1+9+8=18(各位の数の和)、198=9×22
10の倍数の見分け方(=10で割きれるかどうか)
1の位が「0」になっていればその数は10の倍数になる。
例) 「120」 =10×12
7の倍数は2ケタの7の倍数を九九以降もすべて覚えておく!(70,77,84,91,98)
まとめ
算数が得意、問題を解くのが早い人は、こういった知識を豊富に持っています。
知っているのと知らないのでは大きな差がつくので、しっかりと覚えておきましょう!!
10月は約分と通分、分数のたし算とひき算などの学習をします。
小学6年生

【算数】円の面積
6年生は円の面積を中心に学習をしました。面積の求め方はわかるけど計算が全然合わないという人が多かったです。
なかでも、いろいろな面積を求めるときは、普通に計算しようとすると計算ミスがでてしまう可能性が高くなります。
小4でも習った「計算のくふう」を使うことで簡単に計算をすることができるものもあります。
【復習】計算のくふう(小4)
12×9+8×9=(12+8)×9=20×9=180
「いろいろな面積」の例題と解き方
色がついている部分の面積を求めなさい。
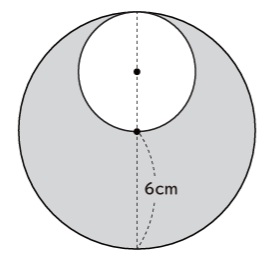
【解答①】普通に計算
6×6×3.14-3×3×3.14
=113.04-28.26
=84.78(㎠)
【解答②】くふうして計算
6×6×3.14-3×3×3.14
=36×3.14-9×3.14
=(36-9)×3.14
=27×3.14
=84.78(㎠)
まとめ
以上のようにくふうして計算することで早く正確に求めることができるようになります!
ぜひ活用してみてください(^^♪
来月はデータの調べ方や比の学習をします。
【中学生】夏期講習の成果報告
中3生|12年連続偏差値爆上がり達成しました!
夏期講習を終え、夏休み最終日に受験をした「Vもぎ(千葉県最大の高校入試会場模擬テスト)」の結果が返ってきました!
リードアップ中3生は、8月末に行われるVもぎで結果を出すこと(自己最高偏差値を出す・志望校にB判定以上)が目標でした。
中3生は【218コマ(10,900分)偏差値アップ集中特訓コース】を全生徒必修のカリキュラムとして、夏期講習を行いました。
リードアップ中3生の夏期講習は、先取り学習を完全に停止し、中1~中3秋までの2年半の5教科すべての学習内容を徹底的に復習しました。
授業はほとんど行わず、“ひたすら演習”です。“実力が本当に身に付く勉強法だけに全振り”です。
その結果、6月模試から8月Vもぎにかけて、偏差値の平均推移が
+7.0アップ!
という結果に!\(*`∀´)人(`∀´*)/イエーイ☆

みんな良い笑顔だ!!!
というわけで、今年の中3生も超大幅偏差値アップを成し遂げてくれました!!!
すばらしい!!!
詳しくは下の記事でご紹介しています!
中1・2生|8月模試の結果
3教科偏差値5以上UPした生徒が8名も出ました!
一部掲載、詳しくはこちらの記事で
| 3科偏差値+9UP↑ | |
| 期間 | 6月→8月 |
| 偏差値 | 51→60 |
| 中学・学年 | 千葉大附中2年生 |
| 3教科偏差値+8UP↑ | |
| 期間 | 6月→8月 |
| 偏差値 | 50→58 |
| 中学・学年 | 磯辺中1年生 |
| 3教科偏差値+7UP↑ | |
| 期間 | 6月→8月 |
| 偏差値 | 45→52 |
| 中学・学年 | 磯辺中1年生 |
| 3教科偏差値+7UP↑ | |
| 期間 | 6月→8月 |
| 偏差値 | 60→67 |
| 中学・学年 | 磯辺中1年生 |
| 3教科偏差値+6UP↑ | |
| 期間 | 6月→8月 |
| 偏差値 | 61→67 |
| 中学・学年 | 千葉大附中2年生 |
【中学生】前期期末テストの成績アップ結果































中1生は前回の前期中間テストですばらしい成績を取れた生徒が大勢いましたが、今回はさらに点数・順位を伸ばす生徒が複数名いました!
また、中1・中2生は夏期講習で「理社激アップ講座」を設けて、(通常授業とは別に)テスト範囲を3周する集中特訓を行いました。

理社の大量演習、そして定期テストでの点数アップを通して「やればできる」という経験ができたのではないかと思います!
中3生も、400点以上取れた生徒が続出しました!ハイレベル!
夏期講習のVもぎでの成果に続き、定期テストでも自己最高順位を取れた生徒が複数でました。

と、良い循環がつくれています!
中学1年生

続いて中1・中2生です!

【英語】疑問詞をつかった疑問文

疑問詞をつかった疑問文について学習しました。
疑問詞は「なに」「どこ」「いつ」などYes,Noではなく具体的なことをたずねたいときに使われます。
疑問詞をつかった疑問文は以下のようにつくります。
「疑問詞+疑問文の形~」
疑問詞の意味を覚えることはもちろん、be動詞と一般動詞の違いやそれぞれの疑問文の作り方を理解しておく必要があります。
また、下記のようなよく出てくる表現は文章で覚えるようにしましょう。
10月中旬から、教科書内容のテスト対策をはじめます。
【数学】比例・反比例

比例・反比例について学習しました。
比例と反比例を学習する前にまずは関数について理解しましょう。
関数とは「ある量の値が決まると、それに応じて別の量の値も決まる関係」を表現するものです。
関数のなかに「比例」と「反比例」があります。
「xが2倍、3倍…になるとyも2倍、3倍…になる」という関係のことを「比例」といいます。
一方で「xが2倍、3倍…になるとyが1/2倍、1/3倍…になる」という関係のことを「反比例」と呼びます。
比例と反比例については、それぞれの式とグラフをあわせて理解できるようにしましょう。
比例の一般式:\( y=ax \)
(\( a \) は比例定数という)
比例のグラフは、次のように直線になります。
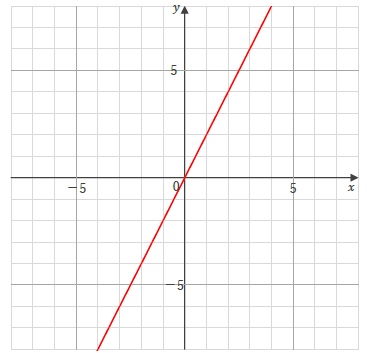
比例のグラフは比例定数 \( a \) が正の数の場合は右上がり、負の場合は右下がりになることも押さえておきましょう。
反比例の一般式:\( \displaystyle y = \frac{a}{x} \)
(\( a \) は比例定数という)
反比例のグラフは、次のように双曲線になります。
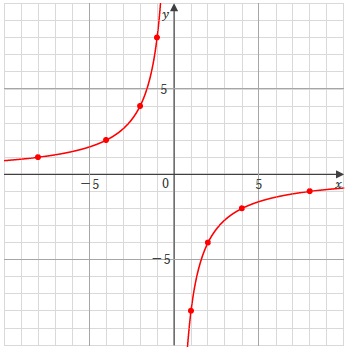
反比例のグラフは、
グラフができます。
比例・反比例は
ということをまずは完璧にできるようにしましょう!!
10月中旬からは、各学校定期テストに向けたテスト範囲の学習に入ります。
中学2年生

【英語】比較

比較について学習しました。
それぞれの形容詞や副詞の比較級、最上級の作り方についてしっかりと覚えるようにしましょう!
比較級・最上級のつくり方
比較級(基本)
形容詞、副詞のもとのかたち(原級)の語尾にerをつける。
| 【原級の語尾】 | (e)rのつけ方 | 例 |
|---|---|---|
| ふつうの語 | erをつける | old→older tall→taller |
| eで終わる語 | rをつける | large→larger nice→nicer |
| 短母音+子音字 | 子音字を重ねてerをつける | big→bigger hot→hotter |
| 子音字+y | yをiにかえてerをつける | happy→happier early→earlier |
最上級(基本)
形容詞、副詞のもとのかたち(原級)の語尾にestをつける。
| 【原級の語尾】 | (e)stのつけ方 | 例 |
|---|---|---|
| ふつうの語 | estをつける | old→oldest tall→tallest |
| eで終わる語 | stをつける | large→largest nice→nicest |
| 短母音+子音字 | 子音字を重ねてestをつける | big→biggest hot→hottest |
| 子音字+y | yをiにかえてestをつける | happy→happiest early→earliest |
最上級にはtheをつけるが、副詞(hard,fastなど)の最上級はtheをつけなくてもよい。
つづりの長い形容詞(副詞)
原級の前にmore,the mostをつける。
不規則に変化する形容詞・副詞
| 【原級】 | 【比較級】 | 【最上級】 |
|---|---|---|
| good [よい] well [上手に] | better | best |
| bad [悪い] | worse | worst |
| many,much [たくさんの] | more | most |
| little [少ない] | less | least |
| far [遠い] | farther | farthest |
まとめ
そのほか「than(~よりも)」「of / in」の使い分けなどもしっかりと覚えましょう。
比較の文は文章も長くなるため、苦手意識をもってしまう生徒も多いです。
日頃の暗唱テストで基本例文を繰り返し練習しましょう!
10月中旬から教科書内容のテスト対策をはじめます。
【数学】1次関数

1次関数について学習しました。
「\( x \) と \( y \) という2つの実数があったとき、\( x \) の値が決まると \( y \) の値も1つに決まる関係」を関数といいます。
\( x \) の値次第で \( y \) の値が決まる関係のことを「\( y \) は \( x \) の関数である」といいます。
このうち「\( y \) を、\( x \) の1次式」で表せるものを1次関数といいます。
1次関数の一般式:「\( y=ax+b \)」
「\( a \)(傾き、変化の割合)とは何か」「\( b \)(切片)とは何か」など、この単元を苦手としてしまう生徒は基本の言葉の意味が十分理解できていないまま問題を解いていることが多いです。
これらの基本の言葉を自分で説明できるようになることがポイントです。
逆にこれらの意味をしっかり理解しておくと、どんな問題でも対応できるようになります。
入試でも頻出かつ苦手にしてしまう生徒が多い単元です。
しっかりとマスターしましょう。
10月中旬からテスト範囲の演習に入ります。
中学3年生

次は中3生です!


英語
関係代名詞(主格・目的格)

関係代名詞について学習しました。関係代名詞は「名詞を修飾するとき」に使います。
関係代名詞の文は次のようにつくります。
「名詞+関係代名詞+節」
例えば主格の関係代名詞では、先行詞が人のときは「who」を、もののときは「which」を使います。
こういった関係代名詞の文法のルールをしっかり覚えることが重要です。
仮定法過去

仮定法過去について学習しました。
仮定法とは「現実の事実に反する事柄を表す表現」で、「もし~なら、……なのに」という文章をつくります。
仮定法過去の文は、次のようにつくります。
「If+過去形, would+原形」
※wouldの部分は正確には「助動詞の過去形」が入ります。
中2のときに学習した「Ifの文」は直接法というものです。
以下の例文を見ながら違いを確認しましょう。
上の文のように、仮定法では「彼女に電話をかけたいのに、実際は彼女の電話番号を知らない」という事実があることがわかります。
このように、仮定法は「現実とは違うことを表現する」ときに使います。
【数学】2次関数
2次関数について学習しました。
「\( x \) が1つに決まれば、それによって \( y \) が1つに決まる」関係を関数といいます(復習)。
このうち、\( y \) が \( x \) の2次式で表されるものを2次関数といいます。
2次関数の一般式:「\( y = ax^2 \)」
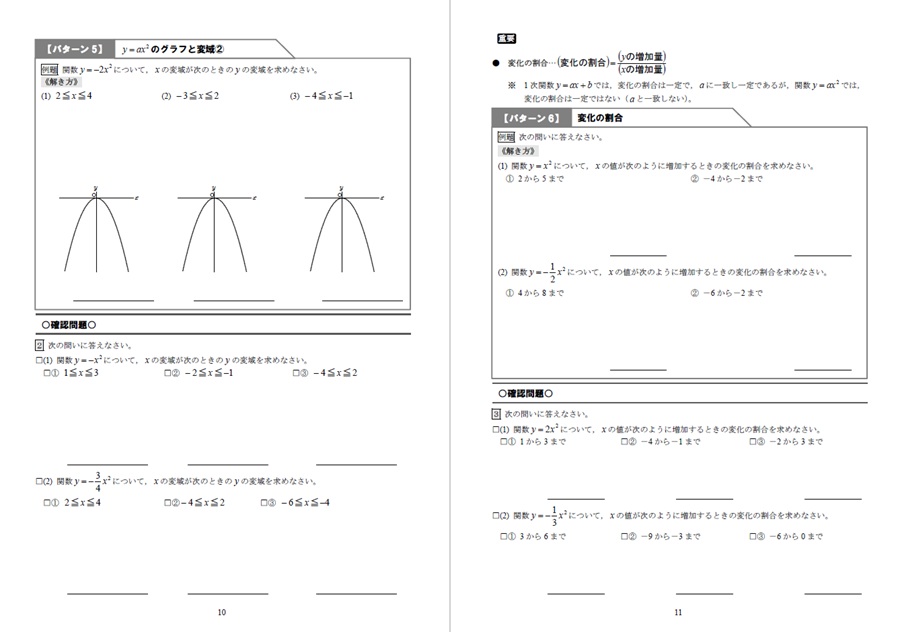
2次関数のグラフは「放物線」とも呼ばれます。
高校入試では、2次関数は「変域」や「変化の割合」の問題が小問集合でよく出題されます。
「変域」や「変化の割合」の問題では、グラフの概形をイメージすることが重要です。頭の中でイメージができなければ、必ず紙にグラフの概形を書くようにしましょう。
9月中に2次関数のテキストを2周やり終えました。
Vもぎ過去問
土曜日の5時間授業を使って、Vもぎの過去問を実施しました。
国語の作文や、英語の英作文などは、講師が一人ひとり個別に添削を行います。
国語の作文のコツ
千葉県の高校入試の作文の問題は
というパターンの問題であることが圧倒的に多いです。
入試だけでなく、中学校の定期テストも同じ形式の問題です。
(学校の先生も高校入試を見越して問題を作ってくれているので)
「作文が苦手」「何を書けばいいかわからない」と悩んでいる人は多いですが、こういった人は「何を書けばいいかわからない=作文は何を書いてもよい」と思ってしまっている場合が多いように感じます。
作文の問題も、あくまで「問題」ですから、ある程度「書くべきこと=正解」というものがあります。
具体的には、上記のパターンの問題であれば
といった風に、「資料から(現代社会の)問題(っぽい)点を読み取り→指摘し→解決策を書く」というのがセオリーです。
あとは作文用紙の使い方はきちんと覚えておきましょう。
英作文
英作文も同様、どんな問題がきても「書くべきこと=正解」が決まっています。
また英作文は「この英単語、わかりますか?ちゃんと書けますか?」問題でもあります。
英作文については、また次回の記事で解説しようと思います!
高校受験情報
敬愛学園の併願推薦復活!(進学コース)
一昨年(現高2生)から無くなっていた、敬愛学園 進学コースの併願推薦が今年の中3から復活します!
我々、検見川浜・稲毛海岸地域の人にとっては、敬愛学園は「数少ない自転車で通える私立高校」ですので、併願推薦復活は朗報ですね!
| 敬愛学園 | A推薦 (単願推薦) | B推薦 (併願推薦) |
|---|---|---|
| 特別進学コース | 5教科21以上 | 5教科23以上 |
| 進学コース | 5教科18以上 | 5教科20以上 |
国語の聞き取り問題が廃止(令和9年度/現中2から)
千葉県の公立高校入試の国語の問題では「聞き取り問題」が出題されていました。(配点は8~10点)
これが、今年の中3で終了。現中2の入試からは聞き取り問題が廃止され、新しい問題が始まります。
本県の令和6年度入学者選抜では、「話すこと・聞くこと」の領域に関して、「放送による聞き取り検査」のみで出題していました。
「放送による聞き取り検査」に代わり、話し合いの場面等を設定した文章による出題とすることで、「話すこと・聞くこと」の領域に関する資質・能力を複数の問題から、見取ることができるようにします。
情報元:千葉県教育員会
【調査書の項目削除】欠席日数関係無し(令和8年度/現中3から)
公立高校入試に関して、今年の中3生の受験から、調査書の下記の4項目が削除されます。
要旨は「欠席日数は一切問わない。不登校の時期があっても大丈夫ですよ」ということです。
これまでは、高校によって「3年間で10日以上の欠席がある場合は審議の対象」といった条件がありました。
こういった「欠席にかかわる条件」は、今後一切なくなります。
配慮の必要な生徒の心理的負担等とならないよう、調査書の記載項目を精選します。削除する項目は、以下の4つとなります。
なお、令和7年度入学者選抜においても、不登校経験を有する生徒について、在籍する学校における出席の状況のみをもって不利益な取扱いをしないこととしています。また、欠席が多い理由について説明するために、自己申告書を提出することができます。自己申告書が提出されたことによって不利益な取扱いをすることはありません。
情報元:千葉県教育員会
高校生

続いて高校生です!

10月の勉強方法
【高3受験生】下から順に過去問演習へ
夏が終わり、9月からは少しずつ過去問に手を付け始められている生徒が出てき始めました。
10月には、全生徒が過去問演習に“少しずつでも”取り組みたいところです。
過去問演習は、偏差値の低い併願校から取り組んで、「合格できる大学」を着実に増やしていくのがおすすめです。
「最低でもこの大学はいけそうだな」とわかる・思えることは、大学受験において精神衛生上、非常に重要です。
過去問は「演習して見直しをして」となると、それなりに時間がかかります。
10~11月は模試もあり、演習できる時間も限られるので、10月から計画的に過去問演習をスタートさせましょう。

国立志望の人は、受験科目も多く、共通テスト対策にも力を抜けませんので、本当に忙しいです。
学校のある日は5時間、休日は12時間以上の勉強時間の確保(起きてる時間すべて)はMUSTです!
【高2生】受験勉強主体に、テス勉を復習として活用しよう
高2の秋はもう、受験勉強もなるべく進めたい大事な時期です。
ですので、定期テスト直前1週間ほど前までは、受験勉強を並行して進めていきたいです。
普段から演習している数学や理科・社会であれば、テスト前だけテスト範囲を取り組むのがおすすめです。
結局入試で出題される範囲なので、テスト勉強を復習の機会として有効活用して、基礎固めをしたいですね。
具体的には、次のような基準でテスト勉強に取り組みましょう。
「定期テストだから」と軽視せずに、受験科目は満点を狙うつもりで取り組んでください。
また、学校によっては10月~11月に修学旅行・文化祭・球技大会などが実施されるところもあります。
学校行事や部活を言い訳にせず、勉強習慣を切らさないよう日々積み上げていきましょう!
【高1生】テスト3週間前には始めて、問題集を3周やろう
3学期制の高校は、10月に中間テストがあります。
定期テストは勉強習慣をつける上で良い機会になりますし、数学や理科・社会、英文法などは定期テストの内容がそのまま受験勉強の基本にもなります。
テストの3週間ほど前から計画的に勉強を進められるよう、予定を立てておきましょう。
入試で使いそうな科目や、1学期に思うように点数が取れなかった科目は、
テストまでに問題集を3周
できるように、逆算して計画を立てましょう。
定期テストにおいて、問題集は学校配布のもの以外は基本的に不要です。
テスト勉強の基準は高2生同様です。
何から勉強を始めればいいかわからない人はリードアップへ!
リードアップでは、生徒ひとりひとりに個別カリキュラムを作成しています。
大学受験勉強の全体像がわかり、受験に向けてやるべきことが明確化されます!

無料体験授業・学習相談を行っているので、「どこから手をつけたらいいか分からない…」という方は、お気軽にご相談ください!
おわりに
以上です!
バックナンバーは下から読めます。


































こんにちは!
検見川浜・稲毛海岸にある進学塾リードアップの山田優輔です。