この記事ではリードアップでの授業内容・学習内容をお伝えします。
塾生でない方は「いまリードアップの授業はどのようなことが行われているのか」をご確認いただけます。
リードアップの塾生・保護者様は学習状況や学習内容をご確認いただき、ご家庭でのお子さんとの会話にご活用いただければと思います。
小学5年生

算数
倍数と約数

5年生は今月は倍数と約数を中心に学校で習っている単元の復習、演習を行いました!
公約数を求めるのに苦戦している生徒が多かった印象です。「公約数を見つけるときは、小さい方の約数の中から、大きい方の公約数を見つける」のがポイントです。
この後習う約分と通分、分数の足し算と引き算でも使う大切な単元となります。苦手な生徒はできるように一緒に頑張りましょう!!
小学6年生

算数
円の面積
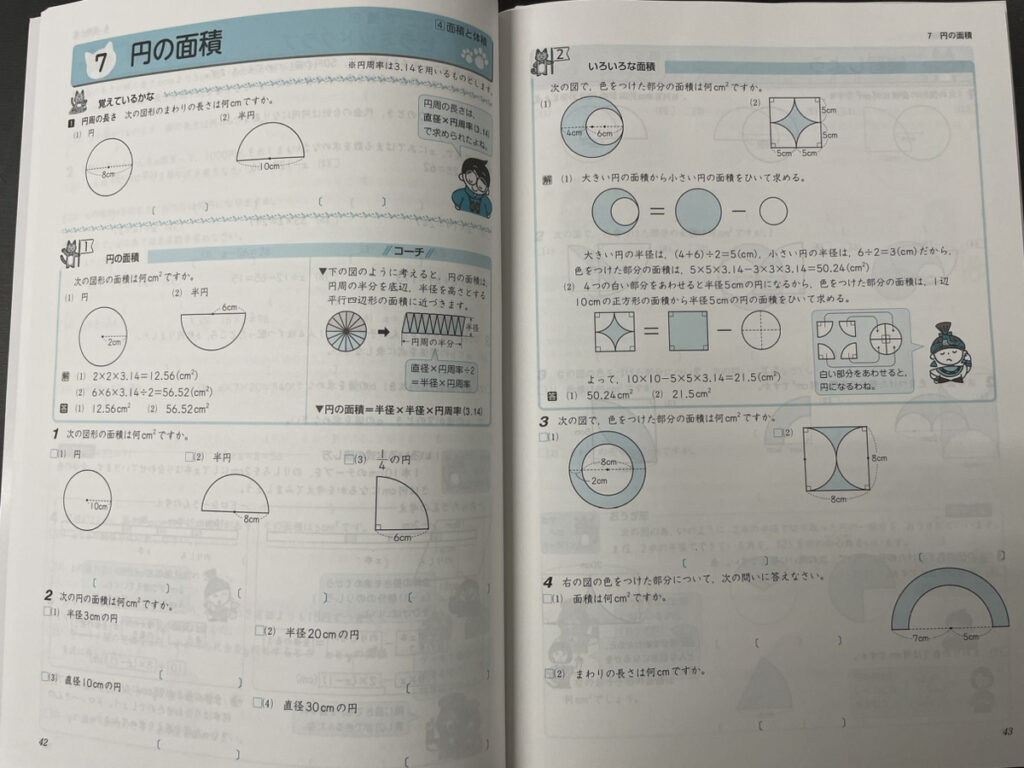
6年生は今月は円の面積を中心に学校で習っている単元の復習、演習を行いました!
苦手な生徒のほとんどは5年生で習った「小数のかけ算」が苦手です。しっかりと復習をしましょう。
円の面積の求め方と円のまわりの長さの求め方を混同している生徒もいました。しっかりと区別するようにしましょう!
この後の角柱や円柱の体積の求め方では円だけではなく、三角形や四角形の面積の求め方もわかっていなければいけません。しっかりと公式を整理して覚えましょう!
中学生前期期末テストの結果


前期期末テストの結果が出そろいました!
今回は前回中間テストで思うような結果が出ずリードアップへ6月、7月に転塾、入塾してくれた生徒の成績アップが目立ちました!
「リードアップに入って勉強量が増えた」「何をどれくらいやればいいのかが明確で取り組みやすい」といったうれしい声を生徒からも保護者様からも頂戴しています。
特に中1,2生は9月以降勉強の内容が難しくなってきます。
「成績があがった!」と油断していると成績をキープするのはおろかあっという間に下がってしまうこともあります。
リードアップでは10月半ばから各学校テスト専用のカリキュラムで対策を開始します!次回定期テストも頑張りましょう!!!
中1・2生8月模試の成績が返ってきました
リードアップでは夏期講習の大きな目標の1つは「英数の苦手を克服し、8月模試で偏差値アップをすること」でした。
今年も多くの生徒が自己最高偏差値を更新することができました!夏期講習お疲れさまでした!!
中学1年生

英語
疑問詞をつかった疑問文

疑問詞をつかった疑問文について学習しました。
疑問詞は「なに」「どこ」「いつ」などYes,Noではなく具体的なことをたずねたいときに使われます。
- What「なに」
- Who「だれ」
- When「いつ」
- Where「どこ」
- Whose「だれの」
- How「どのように」、How old「何歳」、How many 「いくつの」…など
疑問詞をつかった疑問文は以下のようにつくります。
「疑問詞+疑問文の形~」
疑問詞の意味を覚えることはもちろん、be動詞と一般動詞の違いやそれぞれの疑問文の作り方を理解しておく必要があります。
また
- How is the weather today?(今日の天気はどうですか)
- Where are you from?(あなたはどこ出身ですか)
のようなよく出てくる表現は文章で覚えるようにしましょう。
数学
1次方程式

1次方程式について学習しました。
一次方程式とは、式のなかで不明な数字xを求めるための方程式です。
xを使うとむずかしく感じるかもしれませんが、5+☐=9という問題で、☐=9-5=4というのは小学校の知識でも求められますよね。
一次方程式も同様にわからない数字を求めるだけの式なので、その性質を理解すればだれでもできるようになります!
A=Bの場合
- A+C=B+C…等式の両辺に同じ数を足しても等式は成り立つ。
- A-C=B-C…等式の両辺から同じ数を引いても等式は成り立つ。
- A×C=B×C…等式の両辺に同じ数をかけても等式は成り立つ。
- A÷C=B÷C…等式の両辺を同じ数で割っても等式は成り立つ。
上記の性質は理解した上で、問題パターンによってのさまざまな解法を覚えましょう。
「文章題が苦手」という生徒も多いと思いますが、まずは上記のような基本の計算をスムーズに正確に解けるようになることが大切です。
面倒くさがらずに途中式をしっかりと書いて丁寧に計算をするようにしましょう。
途中式を書いておくことで見直しもしやすくなります。
9月中に1次方程式のテキストの1周目をやり終えました。
中学2年生

英語
受動態

受動態について学習しました。受動態とは主語が「〜される」という受け身の状態を表すときに使います。通常の主語が「〜する」という文章は「能動態」といいます。
受動態の文は次のようにつくります。
「be動詞+動詞の過去分詞」
否定文や疑問文はbe動詞の文章と同じようにつくります。
動詞の過去分詞が初めて出てくる単元です。規則動詞、不規則動詞の活用を完璧に覚えることがポイントです。
過去分詞はこの後に習う「現在完了形」などでも出てくるので、過去形と合わせてしっかりと覚えるようにしましょう。
数学
1次関数

1次関数について学習しました。
「xとyという2つの実数があったとき、xの値が決まるとyの値も1つに決まる関係」を関数といいます。xの値次第でyの値が決まる関係のことを「yはxの関数である」といいます。
このうち「yを、xの1次式」で表せるものを1次関数といいます。
1次関数の一般式:「y=ax+b」
「a(傾き、変化の割合)とは何か」「b(切片)とは何か」など、この単元を苦手としてしまう生徒は基本の言葉の意味が十分理解できていないまま問題を解いていることが多いです。
これらの基本の言葉を自分で説明できるようになることがポイントです。
逆にこれらの意味をしっかり理解しておくとどんな問題でも対応できるようになります。
入試でも頻出かつ苦手にしてしまう生徒が多い単元です。しっかりとマスターしましょう。
9月中に1次関数のテキストの1周目をやり終えました。
英検対策講座@準2級・3級
9月は「第2回英検対策講座」を行いました。

全4日間×3hの日程で授業を行いました。
授業内では全パターンの問題演習、解説はもちろんライティング対策、過去問の演習まで一次試験の対策をしっかりと行います。
2024年度からはライティングの問題が1問から2問と増えました。
ライティングは苦手としている生徒が多いですが、英検ではリーディングやリスニングに比べ高得点を狙いやすい問題です。本番までしっかりと練習をして臨んでほしいと思います!
二次試験対策は11月に行います。
一次試験を突破できるように頑張ってください!!!
中学3年生

続いて中3生、高校生です!

英語
関係代名詞(主格・目的格)

関係代名詞について学習しました。関係代名詞は「名詞を修飾するとき」に使います。
関係代名詞の文は次のようにつくります。
「名詞+関係代名詞+節」
例えば主格の関係代名詞では、先行詞が人のときは「who」を、もののときは「which」を使います。
こういった関係代名詞の文法のルールをしっかり覚えることが重要です。
仮定法過去

仮定法過去について学習しました。
仮定法とは「現実の事実に反する事柄を表す表現」で、「もし~なら、……なのに」という文章をつくります。
仮定法過去の文は次のようにつくります。
「If+過去形, would+原形」
※wouldの部分は正確には「助動詞の過去形」が入ります。
中2のときに学習した「Ifの文」は直接法というものです。
以下の例文を見ながら違いを確認しましょう。
上の文のように、仮定法では「彼女に電話をかけたいのに、実際は彼女の電話番号を知らない」という事実があることがわかります。
このように、仮定法は「現実とは違うことを表現する」ときに使います。
数学
2次関数

2次関数について学習しました。
「xが1つに決まれば、それによってyが1つに決まる」関係を関数といいます(復習)。
このうち、yがxの2次式で表されるものを2次関数といいます。
2次関数の一般式:「y=ax2」
2次関数のグラフは「放物線」とも呼ばれます。
高校入試では、2次関数は「変域」や「変化の割合」の問題が小問集合でよく出題されます。
「変域」や「変化の割合」の問題では、グラフの概形をイメージすることが重要です。頭の中でイメージができなければ、必ず紙にグラフの概形を書くようにしましょう。
9月中に2次関数のテキストを2周やり終えました。
Vもぎ過去問
土曜日の5時間授業を使って、Vもぎの過去問を2回実施しました。
国語の作文や、英語の英作文などは、講師が一人ひとり個別に添削を行います。
国語の作文のコツ
千葉県の高校入試の作文の問題は
というパターンの問題であることが圧倒的に多いです。
入試だけでなく、中学校の定期テストも同じ形式の問題です。
(学校の先生も高校入試を見越して問題を作ってくれているので)
「作文が苦手」「何を書けばいいかわからない」と悩んでいる人は多いと思いますが、こういった人は「何を書けばいいかわからない=作文は何を書いてもよい」と思ってしまっている場合が多いように感じます。
作文の問題も、あくまで「問題」ですから、ある程度「書くべきこと=正解」というものがあります。
具体的には、上記のパターンの問題であれば
といった感じで、「資料から(現代社会の)問題(ぽい)点を読み取り→指摘し→解決策を書く」というのがセオリーです。
あとは作文用紙の使い方はきちんと覚えておきましょう。
英作文
英作文も同様、どんな問題がきても「書くべきこと=正解」が決まっています。
また英作文は「この英単語、わかりますか?ちゃんと書けますか?」問題でもあります。
英作文はまた来月の記事で解説しようと思います!
高校生

【実力養成期】解法網羅を行う
高3生は、GMARCHや千葉大・東京都立大志望の生徒が多いのですが、現在は「基礎完成:導入~共通テスト・日東駒専レベル」の次の段階である「実力養成期」に入っています。
実力養成期には「志望校レベルの解法網羅演習」を行います。
解法網羅を終えて、やっと志望校レベルの問題を解く土俵に上がることができます。
解法網羅をやっていないと、そもそも考える土台がないため「解き方が思いつかない」のレベルから抜け出すことができません。
解法網羅に適した教材とは?
解法網羅の教材は、以下のポイントを押さえている必要があります。
この3つの条件を満たせば良質な「問題集」といえます。ですが「問題集」どまりです。
これらの条件に加えて「なぜそう解くのか?をきちんと説明する解説授業がある」というのが理想的です。
参考書だけで学習する場合は、自力で解説を読み解かなければいけません。
そして、解説を読むのは「やればできる」が、スピードの問題で授業があった方が圧倒的に有利です。
「解法の必然性」
解答を見たとき「なぜこの解き方が思いつくんだろう?」となったこと、ありませんか?
解法パターンを学習する際に最も重要なことは「なぜ、この問題をこのように解くのが自然なのか?」という解法の必然性を理解することです。
ですが、参考書や問題集の解答を読んで、この「解法の必然性」を自力で理解するのはかなり難しいです。
仮に参考書を頑張って読んでも「なぜそう解くのか?」は書いておらず、自力で考えても無理だったり、膨大な時間がかかってしまうからです。
これが「独学の壁」です。
予備校に通っていたとしても同じ結末です。
予備校の講座で「難関大・理系数学」という講座があったとして、90分×20コマが普通。難関大の数学をしっかり解説すれば、90分で4~5題が精一杯です。
5題×20コマなら、実は予備校の通年講座1つでは「MAX100題しかやっていない」のです。たったの100題では難関大の数学を解けるようになる訳がありません。解法網羅の数が全く足りていないからです。
結果、「予備校だけでは偏差値が上がらない」という現実を知り、問題集を頑張り始めるのですが、今度は上の「独学の壁」にぶち当たります。
いくら頑張って勉強しても解法網羅がなかなか進まず、志望校レベルの問題が解けるようにはならず、そして一向に偏差値も上がらない…
解法網羅には膨大な時間がかかります。
偏差値を最短最速で上げ、時間との戦いを制さなければいけない受験生に必要なのは、
という一連の思考の流れをきちんと説明してくれるような授業です。さらに、解法網羅を最速でやるために「全問解説授業」である必要があります。
リードアップの授業はこれらの問題を解決した授業になっています。
GMARCH以上の難関大志望の高校生は、ぜひ一度リードアップ体験授業にお越しいただき、実際の授業を体験してください。


























まずは小5・6生、中1・2生です!